题意:给一个n个点的图和一个n个点的树,求图和树上的点一一对应的方案数。(N<=17)
解法:
1.在树的结构上进行tree DP,f[i][j]表示树上点 i 对应图上点 j 时,这个点所在子树的方案数。O(n^3)。2.我们可以发现如果按这个定义进行DP,“一 一对应”的关系挺难保证。若枚举出全排列得到对应关系,这样就C(n,n)=n! 只能拿到暴力分;那么我们就不限制“一 一对应”而改为“一对多”的关系进行tree DP,利用容斥原理达到O(2^n)的复杂度。(P.S.至于为什么用容斥原理我也不清楚,待我弄懂之后我会再更新的。 2个月后的今天 我说:“应该不会有更新了......”≡[。。]≡)
3.这题的容斥原理应用是这样的:用二进制数枚举出每次DP有哪些数没有对应的树上的点,将所有情况下的DP方案数之和按求补集的公式来求就是“所有数都一一对应树上的点”的答案。
下图中圆圈1表示数1没有对应的点的方案数,依次类推。有颜色部分是我们要求的补集。
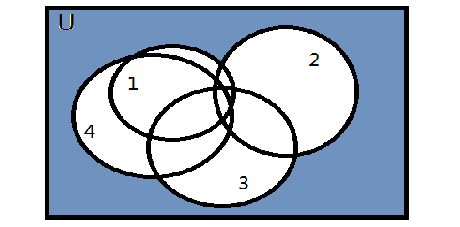
下面附上代码——
1 #include2 #include 3 #include 4 #include 5 using namespace std; 6 7 typedef long long LL; 8 const int N=20,M=400; 9 struct node{ int x,y,next;}a[2*N]; 10 int last[N],len; 11 bool v[N][N],vis[N]; 12 LL f[N][N]; 13 int b[N],bt; 14 15 void add(int x,int y) 16 { 17 len++; 18 a[len].x=x,a[len].y=y; 19 a[len].next=last[x],last[x]=len; 20 } 21 22 void dfs(int x,int fa) 23 { 24 /*for(int k=last[x];k;k=a[k].next) 25 { 26 int y=a[k].y; 27 if(y==fa)continue; 28 dfs(y,x); 29 } 30 for (int kk=1;kk<=bt;kk++) 31 { 32 int i=b[kk]; 33 f[x][i]=1; 34 for (int k=last[x];k;k=a[k].next) 35 { 36 int y=a[k].y; 37 if (y==fa) continue; 38 LL h=0; 39 for (int kkk=1;kkk<=bt;kkk++) 40 { 41 int j=b[kkk]; 42 if (v[i][j]) h+=f[y][j]; 43 } 44 f[x][i]*=h; 45 } 46 }*///边建树,边不重复地DP 47 if (vis[x]) return; 48 for (int kk=1;kk<=bt;kk++) 49 { 50 int i=b[kk]; 51 f[x][i]=1; 52 for (int k=last[x];k;k=a[k].next) 53 { 54 int y=a[k].y; 55 if (y==fa) continue; 56 dfs(y,x); 57 vis[y]=true; 58 LL h=0; 59 for (int kkk=1;kkk<=bt;kkk++) 60 { 61 int j=b[kkk]; 62 if (v[i][j]) h+=f[y][j]; 63 } 64 f[x][i]*=h; 65 } 66 }//打标记,快一点 67 } 68 69 int main() 70 { 71 int n,m; 72 scanf("%d%d",&n,&m); 73 memset(v,false,sizeof(v)); 74 for (int i=1;i<=m;i++) 75 { 76 int x,y; 77 scanf("%d%d",&x,&y); 78 v[x][y]=v[y][x]=true; 79 } 80 memset(last,0,sizeof(last)); 81 len=0; 82 for (int i=1;i